DISTRIBUCIONES

DISTRIBUCION NORMAL

En estadística y probabilidad se llama distribución normal, distribución de Gauss o distribución gaussiana, a una de las distribuciones de probabilidad de variable continua que con más frecuencia aparece aproximada en fenómenos reales.

La gráfica de su función de densidad tiene una forma acampanada y es simétrica respecto de un determinado parámetro estadístico. Esta curva se conoce como campana de Gauss y es el gráfico de una función gaussiana.

La importancia de esta distribución radica en que permite modelar numerosos fenómenos naturales, sociales y psicológicos. Mientras que los mecanismos que subyacen a gran parte de este tipo de fenómenos son desconocidos, por la enorme cantidad de variables incontrolables que en ellos intervienen, el uso del modelo normal puede justificarse asumiendo que cada observación se obtiene como la suma de unas pocas causas independientes.

De hecho, la estadística es un modelo matemático que sólo permite describir un fenómeno, sin explicación alguna. Para la explicación causal es preciso el diseño experimental, de ahí que al uso de la estadística en psicología y sociología sea conocido como método correlacional.

La distribución normal también es importante por su relación con la estimación por mínimos cuadrados, uno de los métodos de estimación más simples y antiguos.

Algunos ejemplos de variables asociadas a fenómenos naturales que siguen el modelo de la normal son:

caracteres morfológicos de individuos como la estatura;
caracteres fisiológicos como el efecto de un fármaco;
caracteres sociológicos como el consumo de cierto producto por un mismo grupo de individuos;
caracteres psicológicos como el cociente intelectual;
nivel de ruido en telecomunicaciones;
errores cometidos al medir ciertas magnitudes;
etc.

La distribución normal también aparece en muchas áreas de la propia estadística. Por ejemplo, la distribución muestral de las medias muestrales es aproximadamente normal, cuando la distribución de la población de la cual se extrae la muestra no es normal.^[] Además, la distribución normal maximiza la entropía entre todas las distribuciones con media y varianza conocidas, lo cual la convierte en la elección natural de la distribución subyacente a una lista de datos resumidos en términos de media muestral y varianza. La distribución normal es la más extendida en estadística y muchos tests estadísticos están basados en una supuesta "normalidad".

La línea verde corresponde a la distribución normal estándar
Función de densidad de probabilidad

DISTRIBUCIONES MUÉSTRALES.

Las muestras aleatorias obtenidas de una población son, por naturaleza propia, impredecibles. No se esperaría que dos muestras aleatorias del mismo tamaño y tomadas de la misma población tenga la misma media muestral o que sean completamente parecidas; puede esperarse que cualquier estadístico, como la media muestral, calculado a partir de las medias en una muestra aleatoria, cambie su valor de una muestra a otra, por ello, se quiere estudiar la distribución de todos los valores posibles de un estadístico. Tales distribuciones serán muy importantes en el estudio de la estadística inferencial, porque las inferencias sobre las poblaciones se harán usando estadísticas muestrales. Como el análisis de las distribuciones asociadas con los estadísticos muestrales, podremos juzgar la confiabilidad de un estadístico muestral como un instrumento para hacer inferencias sobre un parámetro poblacional desconocido.

DISTRIBUCIONES. T.

En probabilidad y estadística, la distribución t (de Student) es una distribución de probabilidad que surge del problema de estimar la media de una población normalmente distribuida cuando el tamaño de la muestra es pequeño.

Función de densidad de probabilidad

Aparece de manera natural al realizar la prueba t de Student para la determinación de las diferencias entre dos medias muestrales y para la construcción del intervalo de confianza para la diferencia entre las medias de dos poblaciones cuando se desconoce la desviación típica de una población y ésta debe ser estimada a partir de los datos de una muestra.

Caracterización
Aparición y especificaciones de la distribución t de Student
La distribución t de Student es la distribución de probabilidad del cociente

$\frac{Z}{\sqrt{V/\nu\ }}$

donde

Z tiene una distribución normal de media nula y varianza 1
V tiene una distribución ji-cuadrado con $\nu\$ grados de libertad
Z y V son independientes

Si μ es una constante no nula, el cociente $\frac{Z+\mu}{\sqrt{V/\nu\ }}$ es una variable aleatoria que sigue la distribución t de Student no central con parámetro de no-centralidad $\mu$ .

Supongamos que X₁,..., X_n son variables aleatorias independientes distribuidas normalmente, con media μ y varianza σ². Sea

$\overline{X}_n=(X_1+\cdots+X_n)/n$

la media muestral. Entonces

$Z=\frac{\overline{X}_n-\mu}{\sigma/\sqrt{n}}$

sigue una distribución normal de media 0 y varianza 1.

Sin embargo, dado que la desviación estándar no siempre es conocida de antemano, Gosset estudió un cociente relacionado,

$T=\frac{\overline{X}_n-\mu}{S_n/\sqrt{n}},$

donde

$S ^ 2(x) = \frac{1}{n-1} \sum_{i=1}^n (x_i - \overline{x}) ^ 2$

es la varianza muestral y demostró que la función de densidad de T es

$f(t) = \frac{\Gamma((\nu+1)/2)}{\sqrt{\nu\pi\,}\,\Gamma(\nu/2)} (1+t^2/\nu)^{-(\nu+1)/2}$

donde $\nu\$ es igual a n − 1.

La distribución de T se llama ahora la distribución-t de Student.

El parámetro $\nu\$ representa el número de grados de libertad. La distribución depende de $\nu\$ , pero no de $\mu$ o $\sigma$ , lo cual es muy importante en la práctica.

Intervalos de confianza derivados de la distribución t de Student

El procedimiento para el cálculo del intervalo de confianza basado en la t de Student consiste en estimar la desviación típica de los datos S y calcular el error estándar de la media $= \frac{S}{\sqrt{n}}$ , siendo entonces el intervalo de confianza para la media = $=\overline{X} \pm t_{\alpha/2,n-1} \frac{S}{\sqrt{n}}$ .

Es este resultado el que se utiliza en el test de Student: puesto que la diferencia de las medias de muestras de dos distribuciones normales se distribuye también normalmente, la distribución t puede usarse para examinar si esa diferencia puede razonablemente suponerse igual a cero.

para efectos prácticos el valor esperado y la varianza son:

E(t(n))= 0 y Var (t(n-1)) = n/(n-2) para n > 3

Distribución t de Student No Estandarizada

La distribución t puede generalizarse a 3 parámetros, introduciendo un parámero locacional $\mu$ y otro de escala $\sigma$ . El resultado es una distribución t de Student No Estandarizada cuya densidad está definida por:^[2]

$p(x|\nu,\mu,\sigma) = \frac{\Gamma(\frac{\nu + 1}{2})}{\Gamma(\frac{\nu}{2})\sqrt{\pi\nu}\sigma} \left(1+\frac{1}{\nu}\left(\frac{x-\mu}{\sigma}\right)^2\right)^{-\frac{\nu+1}{2}}$

Equivalentemente, puede escribirse en términos de $\sigma^2$ (correspondiente a la varianza en vez de a la desviación estándar):

$p(x|\nu,\mu,\sigma^2) = \frac{\Gamma(\frac{\nu + 1}{2})}{\Gamma(\frac{\nu}{2})\sqrt{\pi\nu\sigma^2}} \left(1+\frac{1}{\nu}\frac{(x-\mu)^2}{\sigma^2}\right)^{-\frac{\nu+1}{2}}$

Otras propiedades de esta versión de la distribución t son:^[2]

$\begin{align} \operatorname{E}(X) &= \mu \quad \quad \quad \text{for }\,\nu > 1 ,\\ \text{Var}(X) &= \sigma^2\frac{\nu}{\nu-2}\, \quad \text{for }\,\nu > 2 ,\\ \text{Moda}(X) &= \mu . \end{align}$

DISTRIBUCIONES NORMAL DOS PARÁMETRO

Dado un experimento de variable aleatoria continua X, se llama distribución normal a aquella que queda perfectamente descrita por su media aritmética y su desviación típica s. Las distribuciones normales, también llamadas gaussianas, se denotan por la expresión N ( , s).

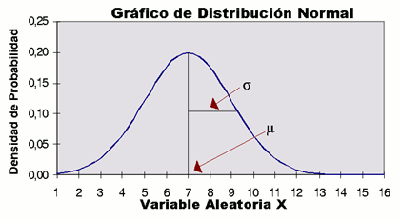
La gráfica de una distribución normal es la conocida campana de Gauss.

Media y desviación típica

Una función de densidad asociada a una distribución normal se caracteriza por dos parámetros complementarios:

La media , que corresponde al punto en el que la función de distribución alcanza un máximo.

La desviación típica s, que señala la anchura de la distribución.

La función que describe una distribución normal presenta puntos de inflexión en las abscisas: - s y + s, donde se modifica la concavidad de la curva. Finalmente, en los valores de la variable estadística que tienden a -¥ y +¥, la función tiende a cero.

DISTRIBUCIONES. T DOS PARÁMETROS

Pruebas t para dos muestras apareadas y desapareadas

Las pruebas-t de dos muestras para probar la diferencia en las medias pueden ser desapareadas o en parejas. Las pruebas t pareadas son una forma de bloqueo estadístico, y poseen un mayor poder estadístico que las pruebas no apareadas cuando las unidades apareadas son similares con respecto a los "factores de ruido" que son independientes de la pertenencia a los dos grupos que se comparan ^{[cita requerida]}. En un contexto diferente, las pruebas-t apareadas pueden utilizarse para reducir los efectos de los factores de confusión en un estudio observacional.

Desapareada

Las pruebas t desapareadas o de muestras independientes, se utilizan cuando se obtienen dos grupos de muestras aleatorias, independientes e idénticamente distribuidas a partir de las dos poblaciones a ser comparadas. Por ejemplo, supóngase que estamos evaluando el efecto de un tratamiento médico, y reclutamos a 100 sujetos para el estudio. Luego elegimos aleatoriamente 50 sujetos para el grupo en tratamiento y 50 sujetos para el grupo de control. En este caso, obtenemos dos muestras independientes y podríamos utilizar la forma desapareada de la prueba t. La elección aleatoria no es esencial en este caso, si contactamos a 100 personas por teléfono y obtenemos la edad y género de cada una, y luego se utiliza una prueba t bimuestral para ver en que forma la media de edades difiere por género, esto también sería una prueba t de muestras independientes, a pesar de que los datos son observacionales.

Apareada

Las pruebas t de muestras dependientes o apareadas, consisten típicamente en una muestra de pares de valores con similares unidades estadísticas, o un grupo de unidades que han sido evaluadas en dos ocasiones diferentes (una prueba t de mediciones repetitivas). Un ejemplo típico de prueba t para mediciones repetitivas sería por ejemplo que los sujetos sean evaluados antes y después de un tratamiento.

Una prueba 't basada en la coincidencia de pares muestrales se obtiene de una muestra desapareada que luego es utilizada para formar una muestra apareada, utilizando para ello variables adicionales que fueron medidas conjuntamente con la variable de interés.^[8]

La valoración de la coincidencia se lleva a cabo mediante la identificación de pares de valores que consisten en una observación de cada una de las dos muestras, donde las observaciones del par son similares en términos de otras variables medidas. Este enfoque se utiliza a menudo en los estudios observacionales para reducir o eliminar los efectos de los factores de confusión.

Cálculos

Las expresiones explícitas que pueden ser utilizadas para obtener varias pruebas t se dan a continuación. En cada caso, se muestra la fórmula para una prueba estadística que o bien siga exactamente o aproxime a una distribución t de Student bajo la hipótesis nula. Además, se dan los apropiados grados de libertad en cada caso. Cada una de estas estadísticas se pueden utilizar para llevar a cabo ya sea un prueba de una cola o prueba de dos colas.

Una vez que se ha determinado un valor t, es posible encontrar un valor P asociado utilizando para ello una tabla de valores de distribución t de Student. Si el valor P calulado es menor al límite elegido por significancia estadística (usualmente a niveles de significancia 0,10; 0,05 o 0,01), entonces la hipótesis nula se rechaza en favor de la hipótesis alternativa.

Prueba t para muestra única

En esta prueba se evalúa la hipótesis nula de que la media de la población estudiada es igual a un valor especificado μ₀, se hace uso del estadístico:

$t = \frac{\overline{x} - \mu_0}{s/\sqrt{n}},$

donde $\overline{x}$ es la media muestral, s es la desviación estándar muestral y n es el tamaño de la muestra. Los grados de libertad utilizados en esta prueba se corresponden al valor n − 1.

DISTRIBUCIONES. F.

La necesidad de disponer de métodos estadísticos para comparar las varianzas de dos poblaciones es evidente a partir del análisis de una sola población. Frecuentemente se desea comparar la precisión de un instrumento de medición con la de otro, la estabilidad de un proceso de manufactura con la de otro o hasta la forma en que varía el procedimiento para calificar de un profesor universitario con la de otro.
Intuitivamente, podríamos comparar las varianzas de dos poblaciones,

, utilizando la razón de las varianzas muestrales s²₁/s²₂. Si s²₁/s²₂ es casi igual a 1, se tendrá poca evidencia para indicar que

no son iguales. Por otra parte, un valor muy grande o muy pequeño para s²₁/s²₂, proporcionará evidencia de una diferencia en las varianzas de las poblaciones.

₁ y

₂ respectivamente.

grados de libertad en el numerador y

grados de libertad en el denominador.

para

_{1 _{2, respectivamente, entonces:üenther, se tendrá que buscar primero los grados de libertad dos para luego localizar el área correspondiente, relacionándola con los grados de libertad uno, para calcular el valor de F.}²}²y
La variable aleatoria F se define como el cociente de dos variables aleatorias ji-cuadrada independientes, cada una dividida entre sus respectivos grados de libertad. Esto es,

donde U y V son variables aleatorias ji-cuadrada independientes con grados de libertad

Sean U y V dos variables aleatorias independientes que tienen distribución ji cuadradas con

grados de libertad, respectivamente. Entonces la distribución de la variable aleatoria

está dada por:

y se dice que sigue la distribución F con

La media y la varianza de la distribución F son:

para

La variable aleatoria F es no negativa, y la distribución tiene un sesgo hacia la derecha. La distribución F tiene una apariencia muy similar a la distribución ji-cuadrada; sin embargo, se encuentra centrada respecto a 1, y los dos parámetros

proporcionan una flexibilidad adicional con respecto a la forma de la distribución.

Si s₁² y s₂² son las varianzas muestrales independientes de tamaño n₁ y n₂ tomadas de poblaciones normales con varianzas

Para manejar las tablas de Fisher del libro de Introducción a la Inferencia Estadística del autor G

Las tablas tienen la siguiente estructura:

	P	1 2 3 ……. ….. 500 …
6	0.0005
	0.001
	0.005
	.
	.
	0.9995	30.4

El valor de 30.4 es el correspondiente a una Fisher que tiene 3 grados de libertad uno y 6 grados de libertad dos con un área de cero a Fisher de 0.995. Si lo vemos graficamente:

=4 y

=9.

=15 y

=10.

=6 y

=8.

=24 y

=24

Como nos podemos imaginar existen varias curvas Fisher, ya que ahora su forma depende de dos variables que son los grados de libertad.

Ejemplos :

Encontrar el valor de F, en cada uno de los siguientes casos:

El área a la derecha de F, es de 0.25 con
El área a la izquierda de F, es de 0.95 con
El área a la derecha de F es de 0.95 con con
El área a la izquierda de F, es de 0.10 con con

Solución:

Como el área que da la tabla es de cero a Fisher, se tiene que localizar primero los grados de libertad dos que son 9, luego un área de 0.75 con 4 grados de libertad uno.
En este caso se puede buscar el área de 0.95 directamente en la tabla con sus respectivos grados de libertad.
Se tiene que buscar en la tabla un área de 0.05, puesto que nos piden un área a la derecha de F de 0.95.
Se busca directamente el área de 0.10, con sus respectivos grados de libertad.